The Big Bang
The modern standard model for the origin of the universe postulates a beginning when all the energy (and energy equivalent of mass) was compressed into a tiny space with extremely high energy density and temperature. You can't think of this an object in a great black emptiness--space itself was very small, and the energy filled all of it. Under the pressure of all this energy, space began to expand. The energy density and the temperature decreased as a result of this expansion. A popular two-dimensional analogy to help explain this strange state of affairs is the surface of a balloon as it is blown up. At the beginning of the inflation, the surface area of the balloon is small, but it is all the "space" that exists. During the inflation, the surface area of the balloon increases, just as the amount of space in the universe increased during the expansion called the "Big Bang."
Nuclear physics started when the temperature of the universe decreased to about 109 K about 200 seconds after the Big Bang. At this time, the currently observed ratio of neutrons to protons "froze out" (about 13% n and 87% p), and the neutrons combined with the protons to form 2H (deuterons), 3He, 4He (alpha particles), and 7Li. The primeval ratios of abundance for these nuclei can still be observed if one avoids regions where the remnant matter from the Big Bang was processed through stars. Theories have been constructed to explain these abundances. They depend on the details of the cross sections for several nuclear reactions and global factors such as ΩB, the total baryon density of the universe (baryons are neutrons and protons). Thus an accurate knowledge of several nuclear reactions, such as t+4He→γ+7Li, allows one to "weigh" the universe (at least the baryonic part)! This allows you to discuss truly great issues, such as whether the universe will continue to expand forever, or whether gravity will cause it to stop expanding and collapse back for another Big Bang. In T-2, we are working on more and more accurate values for the light-ion reaction cross sections using a nuclear modeling technique called the "R-matrix." Information on our light-ion cross sections is available in our astro area. Another compilation of nuclear data for astrophysics is available at LBNL.
The hot mix of H, He, and Li continued expanding and cooling for about 1015 seconds (30 million years), reaching a temperature of 100 K, before the force of gravity began to take over and form galaxies and stars. The current age of the universe is somewhere around 16 billion years (estimates range from 9 to 23 billion years), and the temperature has decreased to 2.76 K (the famous "black-body radiation").
Nuclear Energy Production in Stars
Through mechanisms that are still being debated in the astronomical community, the initially uniform distribution of matter somehow was broken to form the clumps that were the proto galaxies. Inside these galaxies, other clumps began to collapse under gravity into smaller bodies. The compression of this collapse heated the gas until it began to radiate light into the universe, and the darkness suddenly disappeared. These new stars continued to collapse and heat up. After perhaps 10 or 100 million years of this steady collapse, the internal temperature of the new star reached a value of about 10 million degrees (proton energies of about 1 keV), and thermonuclear reactions between the protons in the gas began. These reactions provided new energy to keep the star shining and to keep it from collapsing further. For a comparatively small sun, like ours, the burning of hydrogen can last for 10 billion years. We are about 5 billion years into that period at this time. Large stars can go through their entire life cycle and explode in only 10 million years!
Early in the life of any star, the nuclear fuel is hydrogen. The first reaction is thought to be p+p→d+e++ν, a reaction of very low cross section at energies near 1 keV (it has never been observed in the laboratory). However, there are lots of protons and lots of time, and appreciable amounts of deuterium can eventually build up. This in turn allows reactions like p+d→γ+3He. This can be followed by d+3He→p+4He to complete the fusion of protons into helium. Each step of this process releases energy to power the star (if you want to look up how much energy is liberated by a particular reaction, check out our online qtool). The cross sections of these reactions and other competing reactions are also part of our research using the R-matrix method.
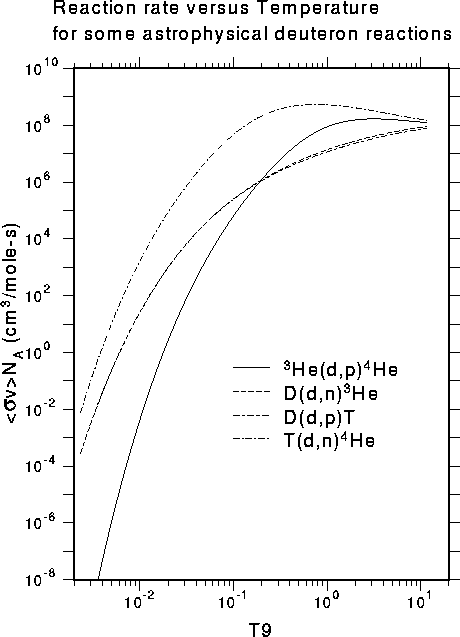
The hot proton gas inside a young star is in thermal equilibrium with some characteristic temperature, such as 107 K. The proton energies are distributed in energy from quite low values up to energies several times as high as the average energy corresponding to the gas temperature (the Maxwell-Boltzmann distribution). The average nuclear reaction rate corresponding to such a distribution requires taking an appropriate integral over the energy-dependent reaction cross section. An example of this kind of reaction rate for several deuteron reactions from our astro area is shown below:
|
The variable "T9" on the abscissa stands for units of 109 K. Note that the reaction rates at the left edge (where hydrogen burning takes place in stars) are quite small. This is largely because of the strong Coulomb repulsion between the positively charged projectile and the positively charged target. These low cross sections around 1 keV are very difficult to measure in the lab using charged particles. The normal approach is to try to measure them at higher energy and then extrapolate to astrophysical energies. However, the R-matrix method used in our group can also take advantage of neutron-induced reactions that lead to the same "compound nucleus." These reactions can be measured at low energies, because the neutron is not repelled by the target nucleus. This application of nuclear theory to the astrophysical problem can reduce the dependence on extrapolation and improve the reliability of the astrophysics data.
Nucleosynthesis in Massive Stars
Most of the elements and isotopes that we see in nature were produced in massive stars (say 10 to 100 times the mass of our sun) and in the supernova explosions that mark the end of their life. Understanding the relative abundances of these elements and isotopes was a great puzzle for astronomy over the last 70 years, and the answer depended greatly on nuclear physics and an ever increasing body of nuclear data. The process by which the matter that makes up our planet and our bodies was generated is called "nucleosynthesis."
The "ashes" of the hydrogen burning stage in a star are 4He nuclei. When enough of the hydrogen has been consumed so that the energy being generated is insufficient to support the weight of the outer regions of the star against the force of gravity, the star begins to contract and heat up. When the temperature increases to about 0.1 to 0.2x109 K, the helium starts to burn, restabilizing the contraction of the star, and turning it into a red giant. Through a tricky series of nuclear reactions, three 4He nuclei combine to form 12C, which then captures another alpha particle in the reaction 4He+12C →γ+16O. Thus, the ashes of the helium burning stage in stellar evolution are just the carbon and oxygen that are so important to life. Our group has been paying special attention to the alpha-Carbon reaction. It is very difficult to measure at low astrophysical energies, and the extrapolation is full of uncertainties. Our R-matrix approach helps to resolve these uncertainties.
In a star 25 times as massive as our sun, the helium burning stage takes about 500,000 years. It then goes through another contraction and begins to burn up the carbon and oxygen. This stage operates at temperatures of 1 to 2 T9, and the ash is mostly 28Si. The important reactions are things like 12C+12C →α+20Ne, which are called "heavy-ion reactions." This stage may only operate for a few hundred years--the end of the massive star's life is very close.
Here is how it is thought to happen. At a temperature of about 4 T9, the silicon starts to burn through a very complex net of reactions. Photodisintegration becomes important at these temperatures, and these "reverse" reactions produce many neutrons, protons, and alpha particles. These particles then bombard the heavier nuclei in the hot core and build up their masses by successive captures. This continual building and destroying of nuclei favors those with the most stability. Because the most stable nuclei known are those near iron, much of the silicon core gets transformed into iron in the space of about 1 day! When the iron core reaches a mass of about the same value as that of our sun, it becomes unstable against gravitational collapse. In a few seconds, it collapses down until the nuclei are pushing against each other--an increase in density by a factor of 100,000. It then bounces, sending an intense shock wave out through the outer regions of the star. This shock blows off 90% of the mass of the star, including all the layers of hydrogen, helium, carbon-oxygen, silicon, and iron--just the stuff that we need to make planets and human bodies.
The silicon burning phase requires information on hundreds of neutron, proton, and alpha reactions, and on their companion photodisintegration reactions. Since the burn is taking place at temperatures around 4 T9, the average particle energies are in the MeV range where laboratory measurements are possible. In addition, there are now very good nuclear model codes with ever improving capabilities of prediction (for example, the GNASH preequilibrium statistical model code in our Group). On the negative side, there are also many very unstable nuclides produced in these processes, and data do not exist for them. In the future, a new radioactive ion beam facility may be able to fill this gap. Another complication is that some of the nuclides may exist in excited states; theoretical work will be needed to predict how the reaction cross sections of excited nuclei differ from those in their ground state. However, a consequence of the equilibrium between forward reactions and their corresponding reverse reaction is that the value of the cross section cancels out, and the equilibrium abundance of the material depends on its binding energy (Q value) and some spin factors. This makes it very important to have comprehensive tables of nuclear masses that include all possible nuclides in the silicon to iron region, even those that are impossible to observe in experiments. Our Group's Finite-Range Droplet Model (FRDM) has demonstrated an ability to compute nuclear masses for unmeasured nuclei. For more information on the Moller-Nix masses, you can look at papers in our Publications Area, or you can use an online HTML form to retrieve the calculated mass (and other parameters) for any nuclide that you desire. The experimental masses are also provided, when available. In addition, we have an interactive HTML form called qtool that allows you to compute reaction Q values from experimental masses backed up by calculated masses when needed.
Nucleosynthesis of Heavy Isotopes
The discussion above conspicuously omits any production of nuclei above about A=70. Where did our gold, tungsten, and uranium come from? Theory suggests that three additional processes may be responsible: a slow sequence of successive neutron absorptions (the s-process), a rapid sequence of neutron absorptions (the r-process), and a rapid sequence of proton absorptions (the rp-process).
In the s-process, one starts with existing iron-group nuclei. Therefore, it would only be expected to take place in second-generation stars that collapsed out of the residue of a previous supernova explosion. A flux of neutrons is required, and it is most likely that these neutrons come from various (α,n) reactions in the helium-burning region of a red giant star. The seed isotope Z,A from the iron region absorbs a neutron, changing from A to A+1. If the new isotope is stable, it can absorb another neutron, going to A+2. If it is unstable, it is assumed that the neutron capture rate is low enough that the nuclide has plenty of time to decay to Z+1 by β- emission before the next capture. The same neutron-absorption process is then repeated for Z+1. Thus, the nuclides produced lie in the "valley of beta stability" of the chart of the nuclides. Analysis shows that the abundance of a nuclide should be inversely proportional to its cross section for absorbing a neutron averaged over the neutron spectrum present during the s-process. This neutron distribution seems to be characterized by an average temperature of about 30 keV. Thus, the nuclear data requirement for the s-process is a good knowledge of (n,γ) cross sections in the energy range from 1 keV to 100 keV for isotopes close to the line of beta stability. Many such cross sections have been measured and evaluated over the years; those that are tabulated in the US-standard nuclear data file ENDF/B-VII can be accessed through our Index to ENDF/B-VII. Some uncertainties remain, and they are good targets for new measurements.
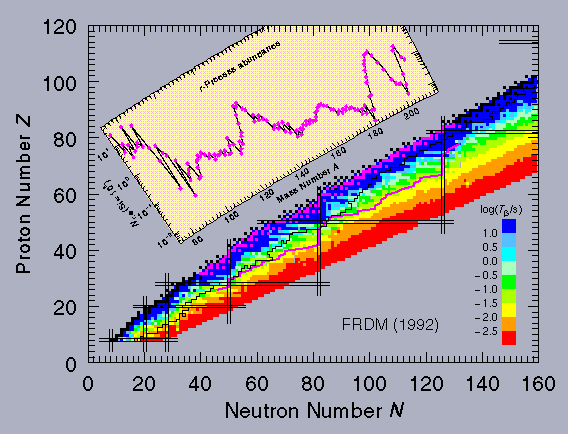
This process cannot explain all of the isotope ratios observed, and the r-process was developed to solve the problem. It also starts with a seed nuclide Z,A from the iron region, and one neutron is absorbed to give A+1. However, in the very rapid r-process, it is assumed that A+1 may not have time to decay before it absorbs another neutron and goes to A+2. This sequence continues moving toward the so-called "neutron drip line" until the probability for absorbing a new neutron is overwhelmed by the probability that a neutron will be knocked off by photodisintegration. This balance point defines the equilibrium A value for this Z. Some of the nuclei will decay to Z+1 by β- emission during this equilibrium and provide a seed for a new series of neutron captures. The path of nucleosynthesis therefore moves up along a line somewhere between the valley of stability and the neutron drip line (the offset depending on conditions such as temperature, neutron flux, and photon flux) until finally fission kills off the chain up in the actinide region. This process clearly requires a huge neutron flux, and it is assumed to take place during the explosion of a supernova. That lasts only a few seconds; when the neutron flux shuts down, all the unstable nuclei produced along the r-process line decay by β- emission to a stable final point. An analysis of this process indicates that the relative abundance of each nuclide should be proportional to the decay lifetime of its progenitor on the r-process line. This is clearly a difficult region to make laboratory measurements! Theory comes to the rescue. The same FRDM that gives the calculated nuclear masses can also be used to estimate beta-decay lifetimes. They are available in tables in papers that can be found in our (Publications Area, or interactively through an online HTML form. A plot of the nuclides contributing to the r-process and the resulting abundances is shown below, superimposed on a representation of β- lifetimes. The small black squares are the stable isotopes, the black line represents the limit of the known nuclides on the neutron-rich side, and the magenta line below and to the right is a typical r-process contour. The small magenta squares show the nuclides that are produced when the r-process line decays.