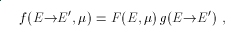
where F is the probability that a neutron will scatter through a laboratory angle with cosine μ irrespective of final energy E'. It is obtained from MF=4. Similarly, g is the probability that a neutron's energy will change from E to E' irrespective of the scattering angle, and it is given in MF=5. Continuum reactions are easily identified by MT numbers of 6-49 and 91. The secondary-energy distributions can be represented using a two-dimensional tabulation or using an analytic law. The feed functions for continuum scattering are simply

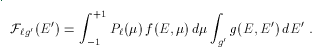
and the cosine omega is related to secondary energy E' by

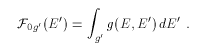
As discussed in the companion article in this volume "An Introduction to the ENDF Formats," the separability assumption is no longer considered adequate for reaction like (n,2n) or (n,n'α), because it doesn't describe the energy-angle correlation that occurs for these reactions. As a result, the continuum approach is only found for old carry-over materials and for minor actinides or fission products where neutron transport is a secondary concern. In these cases, the angular distribution is almost invariably given as isotropic in the laboratory system. However, the continuum approach remains the method of choice for fission, which is also modeled as isotropic in the laboratory frame. Therefore, in almost all cases of interest, the feed function reduces to

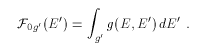
The integrals on the right hand side are returned by the GROUPR subroutine GETSED (for get secondary energy distribution), which either interpolates and integrates over the tabulation, or uses direct analytical integrals, as required. The integration over incident energy proceeds as for all other GROUPR quantities. The result in a scattering or fission matrix, σ_gg'. For scattering, the matrix will contain only downscattering elements for groups g from the threshold up. For fission, the matrix can be almost completely full with both energy increase and energy loss elements.