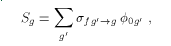
Most existing transport code packages are not able to use a full fission matrix directly to compute this fission source; instead they count on the observation that, except for relatively high neutron energies, the spectrum of fission neutrons is only weakly dependent on initial energy. Therefore, the fission source can be written

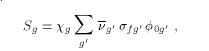
where nu_g is the fission neutron yield, σ_fg is the fission cross section, and χ_g is the average fission spectrum (the familiar "chi" vector), which can be defined by

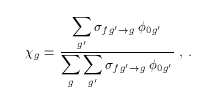
The fission neutron yield is given by

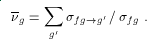
Clearly, χ_g computed in this way depends on the flux in the system of interest. In most cases, the built in weighting functions in GROUPR are not adequate for computing χ_g; they are really only intended to provide reasonable intragroup fluxes. For this reason, GROUPR does not attempt to compute the fission chi itself--it just passes on the full fission matrix to some subsequent code that allows the user to enter an appropriate flux spectrum. Because the energy dependence is weak except for high incident energies, a rough guess for φ_0g usually gives an accurate fission chi. When this is not the case, the problem can be iterated. The DTFR and WIMSR modules know how to calculate chi from GROUPR output, and the TRANSX code working with MATXS files can support the fission-spectrum iteration described above.

There is an addition complication for fission. The fission matrix from GROUPR only describes the prompt part of fission. It is also necessary to obtain the delayed neutron yield and spectra from GROUPR and combine them with the prompt matrix to contain the complete total fission nubar and chi.