GROUPR:
Two-Body Scattering




Elastic scattering (ENDF MT=2) and discrete inelastic neutron scattering (with MT=51-90) are both examples of two-body kinematics and are treated together by GROUPR. The feed function required for the group-to-group matrix calculation may be written
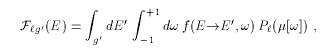
Two-Body Feed Function

where f(E,E',ω) is the probability of scattering from E to E' through a center-of-mass cosine ω and Pls is a Legendre polynomial for laboratory cosine μ. The laboratory cosine corresponding to ω is given by

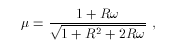
Lab Cosine

and the cosine ω is related to secondary energy E' by

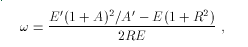
Lab Secondary Energy

where A' is the ratio of the emitted particle mass to the incident particle mass (A'=1 for neutron scattering). In these equations, R is the effective mass ratio

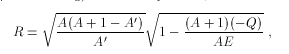
Lab Secondary Energy

where A is the ratio of target mass to neutron mass, and -Q is the energy level of the excited nucleus (Q=0 for elastic scattering). Integrating the defining equation for the two-body feed function over secondary energy gives

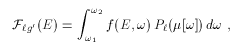
Integrated Feed

where ω1 and ω2 are evaluated using the kinematics equations with E' equal to the upper and lower bounds of g', respectively. The scattering probability is given by

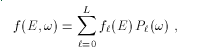
Scattering Probability

where the Legendre coefficients are either retrieved directly from the ENDF/B File 4 or computed from File 4 tabulated angular distributions using subroutines from the GROUPR module called GETFLE and GETCO.

The integration over ω is performed simultaneously for all Legendre components using Gaussian quadrature. The quadrature order is selected based on an estimate of the polynomial order of the integrand using the known order of the CM angular distribution plus a factor depending on atomic weight ratio AWR. More terms are needed for light targets.

The resulting two-body feed function for higher Legendre orders is a strongly oscillatory function of incident energy in some energy ranges. Such functions are very difficult to integrate with adaptive techniques. Gaussian methods, on the other hand, are capable of integrating such oscillatory functions exactly if they are polynomials. Since a polynomial representation of the feed function is fairly accurate, a Gaussian quadrature scheme was chosen for GROUPR. The scheme used is also well adapted to performing many integrals in parallel. In GROUPR, all Legendre components and all final groups are accumulated simultaneously. NJOY takes pains to locate the "critical points" in incident energy so that the Gaussian integrations are performed over energy ranges that do not contain discontinuities. Here is an example of a multigroup elastic scattering matrix for carbon computed using GROUPR for a 30-group structure: 

         group constants at t=3.000E+02 deg k                                    16.6s
         for mf  6 and mt  2 elastic
    
         initl  final  group constants vs legendre order
         group  group  0          1          2          3

           1      1    8.087E+00  4.532E-01  1.144E-02  4.205E-05
           2      1    7.572E-01 -2.232E-01 -1.690E-02 -4.363E-04
           2      2    4.003E+00  4.900E-01  2.363E-02  4.544E-04
           3      2    7.525E-01 -2.219E-01 -1.676E-02 -4.303E-04
           3      3    3.995E+00  4.879E-01  2.348E-02  4.484E-04
           4      3    7.574E-01 -2.234E-01 -1.686E-02 -4.318E-04
           4      4    3.985E+00  4.891E-01  2.357E-02  4.498E-04
           5      4    7.539E-01 -2.223E-01 -1.678E-02 -4.294E-04
           5      5    3.986E+00  4.880E-01  2.348E-02  4.474E-04
             ...
          28     26    8.308E-02 -4.928E-02  8.439E-03  1.234E-02
          28     27    2.545E-01  7.532E-02 -6.513E-03  2.423E-02
          28     28    5.256E-01  4.740E-01  3.849E-01  2.805E-01
          29     26    4.329E-03 -4.075E-03  3.606E-03 -2.988E-03
          29     27    1.217E-01 -4.973E-02 -1.258E-02  1.592E-02
          29     28    1.841E-01  1.053E-01  2.710E-02  4.737E-04
          29     29    5.124E-01  4.633E-01  3.788E-01  2.799E-01
          30     27    2.721E-02 -2.127E-02  1.255E-02 -5.134E-03
          30     28    6.865E-02 -1.719E-02 -1.846E-02  1.032E-02
          30     29    1.834E-01  1.016E-01  1.937E-02 -7.491E-03
          30     30    6.055E-01  5.428E-01  4.372E-01  3.182E-01

Note that the "in-group" cross section is much larger than the outscattering cross section, which is normally limited to a fairly small energy loss by kinematics. Also note that the scattering tends to be fairly isotropic at low energies (low group numbers here), but it becomes very forward peaked for in-scatter in group 30. This is demonstrated by the slow decrease for higher Legendre orders (a delta function of forward scattering would have the same cross section for each l order).

NEXT
INDEX

23 January 2013 T-2 Nuclear Information Service ryxm@lanl.gov