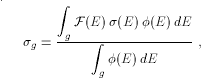
where the integrals are over all initial neutron energies in group g, σ(E) is a cross section at E, and φ(E) is an estimate of the flux at E. We call fancy F of Ethe "feed function". It alone changes for different data types. To average a neutron cross section, fancy F is set to 1. To average a ratio quantity like fission mubar with respect to elastic scattering, fancy F is set to mu. For photon production, fancy F is the photon yield. For matrices, it is the l-th Legendre component of the normalized probability of scattering into secondary energy group g' from initial energy E. This definition is clearly independent of whether the secondary particle is a neutron or a photon.

The question of integration grid or quadrature scheme is important for the evaluation this equation. Each factor in the integrands has its own characteristic features, and it is important to account for them all. First, a grid must be established for each factor. As an example, the grid of σ(E) is generated in RECONR and BROADR such that sigma can be obtained to within a given tolerance by linear interpolation. GROUPR contains a subroutine GETSIG which carries out this interpolation at E and also returns the next grid energy in ENEXT. Subroutines GETFLX and GETFF perform similar functions for the flux and feed function. It is now easy to generate a union grid for the three-factor integrand by just selecting the next closest ENEXT from all the factors at each step of the integration.