GROUPR:
Multigroup Constants




It is very time consuming to carry out full calculations of neutron transport using the detailed PENDF cross sections that we have discussed in the preceding pages, although it can be done using continuous-energy Monte Carlo codes like MCNP, which we will discuss later. Therefore, it is very common to reduce the detail in the cross sections by averaging them over a set of energy ranges called "groups." The GROUPR module of the NJOY system carries out such averages for the pointwise cross sections, and it also generates multigroup "matrices," which describe the transfer of neutrons from one group to another.

The basis for GROUPR is the "multigroup Boltzmann transport equation," which can be written as

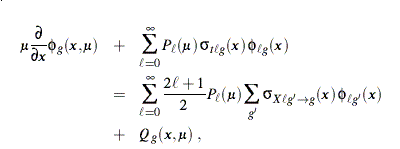
Multigroup Boltzman Equation

where slab geometry has been used for simplicity. The first term describes the spatial transport of neutrons in group g, the second accounts for reactions in group g, the third gives the source into group g from other groups, and the last includes any fixed sources and the source from fission. The flux and cross sections that appear here are defined as follows:

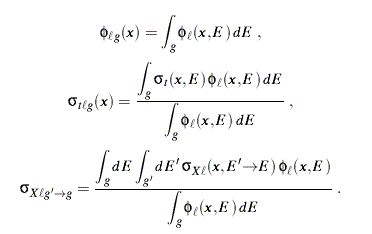
Transport Cross Sections

One of the reasons for doing a transport calculation is to obtain various "responses," such heating, production of a radionuclide, or production of helium. The responses can be computed using the multigroup flux together with a multigroup reaction cross section:

Reaction Cross Section

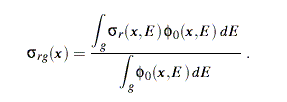
It is the mission of GROUPR to compute the cross sections with "g" subscripts, which are often called "multigroup constants." The Boltzmann equation itself is then solved in a separate neutron transport code, such as ANISN or DANT.


NEXT
INDEX

23 January 2013 T-2 Nuclear Information Service ryxm@lanl.gov