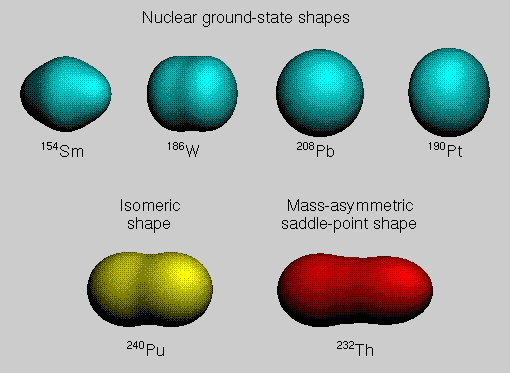
Nuclear Structure

where this isotope of iron has Z=26 and A=56, and where the suffix "m" denotes an isomer. Thousands of nuclei have been observed in nature or in the laboratory. About 300 of them are stable, but most are radioactive and decay into stable isotopes or other radioactive isotopes with some characteristic half life. (The half life is the time required for half of an initial sample of radioactive isotope to decay away. For a half life of one year, half will be gone in 1 year, three fourths in two years, seven eigths in three years, and so on.) Theory says that there are many more possible nuclides, for a total of perhaps 5000 species, but these additional isotopes have such short half lives that they have not been observed in the laboratory. However, even these fleeting nuclei have their effects in processes like stellar nucleosynthesis.

In analogy with the familiar Periodic Chart of the Atoms, there is a Chart of the Nuclides. The standard chart is arranged with Z as the vertical axis (increasing upwards) and N as the horizontal axis. For an example on the net, see the JAEA chart. The Chart of the Nuclides is also available as a book or a wall chart.

Because of the importance of nuclear mass as a basic property, a lot of work has been put into measuring masses and into constructing theories for predicting masses. For the current status on measured masses, consult G. Audi and A. H. Wapstra, Nucl. Phys. A595 (1995), 409. Members of our Group have put effort into the theoretical fitting of measured masses and prediction of unmeasured masses. The "Finite Range Droplet Model" (FRDM) has proved very successful; see Nuclear Ground-State Masses and Deformations, by P. Möller, J. R. Nix, W. D. Myers, and W. J. Swiatecki in Atomic Data Nucl. Data Tables 59 (1995), 185-381. The report (and its extensive illustrations) is available from our Publications Area here. For the convenience of users around the world, we provide easy access to both experimental and calculated nuclear masses by means of an online HTML form. Note that theoretical values are only provided for ¹⁶O and up. Nuclear physicist are fond of using energy units to represent masses (through Einstein's E=mc²). Thus, you will notice that atomic masses, nuclear masses, total binding energies, and so on, are given in GeV or MeV. The tables produced by the online form also give the atomic mass in the normal "mass units" (u) of chemistry, namely the mass of the C-12 nucleus divided by 12. In addition, neutron physicists and nuclear engineers like to measure things in units of neutron masses, and those values are given also.

• Beta decay -- this is a very common decay mode where positive or negative electrons (β⁺ or β^-) are emitted, together with associated neutrinos and gamma rays. The betas have very short range, and they are only dangerous if the radionuclide is ingested. The associated gammas can be dangerous (or useful) even outside of the body. As an example, the 5.27-year β^- activity of ⁶⁰Co has some strong gamma-rays that have been used for many applications, from medical therapy to sterilizing food.

• Alpha decay -- this type of decay is common for every heavy nuclei. For example, the radon gas that can be a hazard in homes or mines is an alpha emitter. Alpha particles are charged, and they have very short range. Although they won't penetrate the skin, they become dangerous when ingested (for example, they can cause cancer when they lodge in the lungs).

• Delayed neutrons -- a number of the radioactive fission products can decay by emitting neutrons. These "delayed neutrons" are very important in improving the controllability of nuclear reactors.

• Isomeric decay -- some radionuclides exist in comparatively long-lived excited states known as "isomers." As an example, the isomer of ²⁴²Am has a half life of 141 years, but the ground state decays with a half life of only 16 hours. When an isomer decays, the excitation energy is usually emitted as a gamma ray.

where N₀ is the original number in the sample. The time required for half of the original nuclei to decay is called the "half life;" it is given by

Therefore, the radionuclide will never really be gone, but after many half lives, it will be so rare as to become negligible. If more than one decay mode is available for a nuclide, the total λ will be the sum of the decay rates for each of the decay channels.

In order to better understand the physics of nuclear structure, and because of the technological importance of radioactivity, the decay rates and radioactive emissions from unstable nuclei have been studied intensively. The literature for this active field is summarized in a bibliography called "Nuclear Science References" (NSR) available at the National Nuclear Data Center (NNDC). These data are gathered together and evaluated by the members of the Nuclear Stucture and Decay Data Network. The evaluations make an attempt to come up with a consistent set of "best" data for each nuclide. The result is the Evaluated Nuclear Structure Data File, ENSDF, which is maintained at the NNDC. Printed information that has resulted from this evaluation project is also available in the Table of Isotopes books, which have recently been upgraded and published by John Wiley & Sons.

The material described in the preceeding paragraph has a scientific slant. For applications purposes, it is useful to convert the basic physics data into more observable quantities, such as emission spectra, and to provide them in computer readable form. This is the purpose of the Decay Data Sublibrary of the Evaluated Nuclear Data Files (ENDF). The latest version of the ENDF work is ENDF/B-VII.1. The base files and the formats manual are available through the NNDC. However, we provide a more convenient interface here. It interprets the obscurities of the ENDF format into easily readable HTML pages. To get access to these data, go through our Data Area to the ENDF/B section. The direct link is here. This will give you a page containing a list of all the nearly 4000 nuclides available. Select the desired nuclide to get a new page describing the decay data.

Nucleons orbit around the center of a nucleus within imaginary shells of increasing radius, like the layers of an onion. Nucleons in the outer shells are more energetic than those in the inner shells. A given shell can hold only a certain number of protons or neutrons, and when a shell is filled, additional nucleons must go into the next shell of larger radius and higher energy. A nucleus with a completely filled shell of protons or neutrons is spherical in shape, but other nuclei are deformed, with shapes that are either prolate like an egg or oblate like a pumpkin. Such deformed shapes arise because these nuclei can lower their energy somewhat by rearranging their protons and neutrons into deformed shells accommodating a different number of nucleons.

The top row of the figure shows four nuclear ground-state shapes calculated on the basis of the macroscopic-microscopic method. The macroscopic contributions are calculated with the finite-range droplet model, and the microscopic shell and pairing corrections are calculated from a realistic, diffuse-surface, folded-Yukawa single-particle potential by use of Strutinsky's method. The bottom left-hand portion of the figure shows a shape of a metastable fission isomer, which is trapped at a secondary minimum existing between inner and outer fission saddle points in a multi-dimensional deformation space. The bottom right-hand portion of the figure shows a mass-asymmetric shape of a nucleus as it passes over its last saddle point enroute to fission.