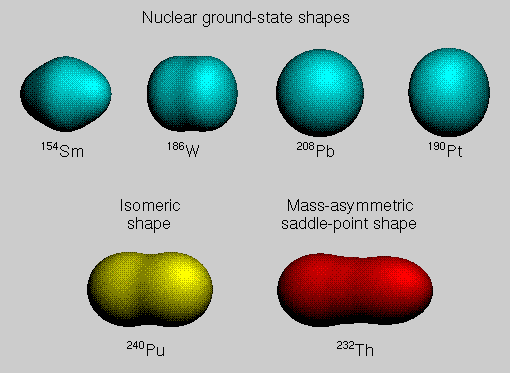
|
Nuclear structure studies the properties of nuclei in isolation
(for interactions between nuclei and radiation, see
nuclear reactions), such as nuclear mass,
characteristic energy levels, and radioactive decay modes.
|
|
Nuclei are named by the element that they belong to (chemical
symbol and/or atomic charge number Z, which is equal to the number
of protons in the nucleus), the nuclear mass number A (which is the
sum of the number of protons and the number of neutrons), and
sometimes an isomeric state of increased energy. The neutron
number N=A-Z is also sometimes used to label nuclei. A number of
different notations will be found, for example:
where this isotope of iron has Z=26 and A=56, and where the suffix "m" denotes an isomer. Thousands of nuclei have been observed in nature or in the laboratory. About 300 of them are stable, but most are radioactive and decay into stable isotopes or other radioactive isotopes with some characteristic half life. (The half life is the time required for half of an initial sample of radioactive isotope to decay away. For a half life of one year, half will be gone in 1 year, three fourths in two years, seven eigths in three years, and so on.) Theory says that there are many more possible nuclides, for a total of perhaps 5000 species, but these additional isotopes have such short half lives that they have not been observed in the laboratory. However, even these fleeting nuclei have their effects in processes like stellar nucleosynthesis. In analogy with the familiar Periodic Chart of the Atoms, there is a Chart of the Nuclides. The standard chart is arranged with Z as the vertical axis (increasing upwards) and N as the horizontal axis. For an example on the net, see the JAEA chart. The Chart of the Nuclides is also available as a book or a wall chart. |
|
One of the most fundamental properties of a nucleus is its mass. The
mass is not just the sum of the masses of its constituent particles.
As an example, Fe-56 contains 26 protons and 30 neutrons. The sum of
the masses of 26 hydrogen atoms and 30 neutrons is 52.59530904 GeV, but
the observed atomic mass is 52.10305516 GeV. The difference is the
"binding energy" of 492.25388 MeV. This is a large binding energy;
Fe-56 is one of the most stable isotopes known. By contrast, the
binding energy of H-2 (the deuteron) is only 2.22 MeV. These binding
energies have a great impact on our understanding of the formation of
the elements and isotopes during the history of the universe. In
addition, the differences in mass between nuclides involved in nuclear
reactions provides the energy that is used or released in the reaction
(the reaction "Q value"). Because of the importance of nuclear mass as a basic property, a lot of work has been put into measuring masses and into constructing theories for predicting masses. For the current status on measured masses, consult G. Audi and A. H. Wapstra, Nucl. Phys. A595 (1995), 409. Members of our Group have put effort into the theoretical fitting of measured masses and prediction of unmeasured masses. The "Finite Range Droplet Model" (FRDM) has proved very successful; see Nuclear Ground-State Masses and Deformations, by P. Möller, J. R. Nix, W. D. Myers, and W. J. Swiatecki in Atomic Data Nucl. Data Tables 59 (1995), 185-381. The report (and its extensive illustrations) is available from our Publications Area here. For the convenience of users around the world, we provide easy access to both experimental and calculated nuclear masses by means of an online HTML form. Note that theoretical values are only provided for 16O and up. Nuclear physicist are fond of using energy units to represent masses (through Einstein's E=mc2). Thus, you will notice that atomic masses, nuclear masses, total binding energies, and so on, are given in GeV or MeV. The tables produced by the online form also give the atomic mass in the normal "mass units" (u) of chemistry, namely the mass of the C-12 nucleus divided by 12. In addition, neutron physicists and nuclear engineers like to measure things in units of neutron masses, and those values are given also. |
Another basic property of nuclei is lifetime. Some nuclei are stable,
but most are radioactive--they decay into other nuclei by emitting
characteristic radiation. There are some naturally occuring radioactive
materials, such as uranium, that have not had time to completely decay
away since the elements were created in some supernova billions of years
ago. Other radionuclides, such as K-40, are always around because of
cosmic rays. With modern technology, we produce many radioactive
species, some by intent (such as radionuclides for medical applications),
and some by accident (fission-product wastes from power reactors, or
activated materials around accelerators). For either class of materials,
it is important to have accurate and comprehensive information about
decay half lives and characteristic emissions. The decay modes
possible for radioactive nuclides include:
where N0 is the original number in the sample. The time required for half of the original nuclei to decay is called the "half life;" it is given by Therefore, the radionuclide will never really be gone, but after many half lives, it will be so rare as to become negligible. If more than one decay mode is available for a nuclide, the total λ will be the sum of the decay rates for each of the decay channels. In order to better understand the physics of nuclear structure, and because of the technological importance of radioactivity, the decay rates and radioactive emissions from unstable nuclei have been studied intensively. The literature for this active field is summarized in a bibliography called "Nuclear Science References" (NSR) available at the National Nuclear Data Center (NNDC). These data are gathered together and evaluated by the members of the Nuclear Stucture and Decay Data Network. The evaluations make an attempt to come up with a consistent set of "best" data for each nuclide. The result is the Evaluated Nuclear Structure Data File, ENSDF, which is maintained at the NNDC. Printed information that has resulted from this evaluation project is also available in the Table of Isotopes books, which have recently been upgraded and published by John Wiley & Sons. The material described in the preceeding paragraph has a scientific slant. For applications purposes, it is useful to convert the basic physics data into more observable quantities, such as emission spectra, and to provide them in computer readable form. This is the purpose of the Decay Data Sublibrary of the Evaluated Nuclear Data Files (ENDF). The latest version of the ENDF work is ENDF/B-VII.1. The base files and the formats manual are available through the NNDC. However, we provide a more convenient interface here. It interprets the obscurities of the ENDF format into easily readable HTML pages. To get access to these data, go through our Data Area to the ENDF/B section. The direct link is here. This will give you a page containing a list of all the nearly 4000 nuclides available. Select the desired nuclide to get a new page describing the decay data. |
|
The shape of a nucleus in its ground state or in a metastable state can be
calculated by minimizing the nuclear potential energy of deformation with
respect to an appropriate set of deformation coordinates. Nuclear ground-state
shapes can be conveniently described in terms of the Nilsson ε
coordinates defined in terms of a perturbation about a
spheroid (an ellipsoid of revolution). These ε coordinates
are related to the β coordinates defined in terms of an expansion of the
radius vector to the nuclear surface in a series of spherical harmonics.
Nucleons orbit around the center of a nucleus within imaginary shells of increasing radius, like the layers of an onion. Nucleons in the outer shells are more energetic than those in the inner shells. A given shell can hold only a certain number of protons or neutrons, and when a shell is filled, additional nucleons must go into the next shell of larger radius and higher energy. A nucleus with a completely filled shell of protons or neutrons is spherical in shape, but other nuclei are deformed, with shapes that are either prolate like an egg or oblate like a pumpkin. Such deformed shapes arise because these nuclei can lower their energy somewhat by rearranging their protons and neutrons into deformed shells accommodating a different number of nucleons. The top row of the figure shows four nuclear ground-state shapes calculated on the basis of the macroscopic-microscopic method. The macroscopic contributions are calculated with the finite-range droplet model, and the microscopic shell and pairing corrections are calculated from a realistic, diffuse-surface, folded-Yukawa single-particle potential by use of Strutinsky's method. The bottom left-hand portion of the figure shows a shape of a metastable fission isomer, which is trapped at a secondary minimum existing between inner and outer fission saddle points in a multi-dimensional deformation space. The bottom right-hand portion of the figure shows a mass-asymmetric shape of a nucleus as it passes over its last saddle point enroute to fission. |
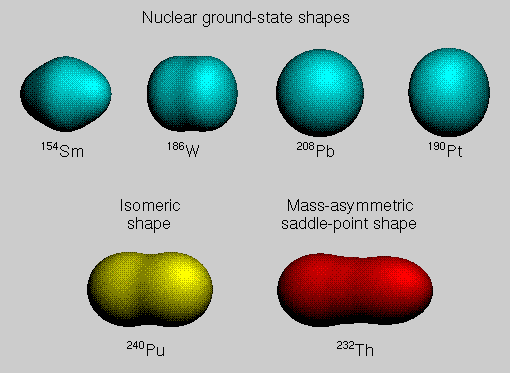
|
| The coordinates that describe the ground-state shapes are available through the same interface that returns the nuclear masses; just look for the deformation table. |