We define the following parameters:

σ_cd (μ,E)

differential Coulomb scattering cross section (barns/sr) for distinguishable particles

σ_ci (μ,E)

cross section for identical particles

E

energy of the incident particle in the laboratory system (eV)

μ

cosine of the scattering angle in the center-of-mass system

m₁

incident particle mass (AMU)

Z₁, Z₂

charge numbers of the incident particle and target, respectively

s

spin (identical particles only, s = 0, 1/2, 1, 3/2, etc.)

A

target/projectile mass ratio

k

particle wave number (barns^-1/2)

eta

dimensionless Coulomb parameter

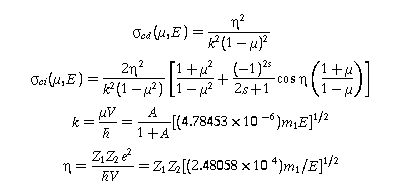
Note that A=1 and Z₁ = Z₂ for identical particles. In the equation for k, μ is the reduced mass. The symbol V represents the relative velocity. The constants in the last two equations are reduced to numerical form with our choice of units for the user's convenience.

The net elastic scattering cross sections for distinguishable and identical particles are as follow:

where the a_l are complex coefficients for expanding the trace of the nuclear scattering amplitude matrix, and the b_l are real coefficients for expanding the nuclear scattering cross section. The value of NL represents the highest partial wave contributing to nuclear scattering. Note that the following holds:

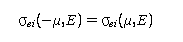
The three terms in the equations for the net elastic cross section are Coulomb, interference, and nuclear scattering, respectively. Since an integrated cross section is not defined for this representation, a value of 1.0 is used in File 3.

When only experimental data are available, it is convenient to remove the infinity due to σ_C by subtraction and to remove the remaining infinity in the interference term by multiplication, thereby obtaining the residual cross section representation:

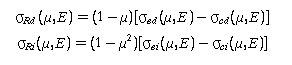
The σ_R can be given as Legendre expansions in the forms

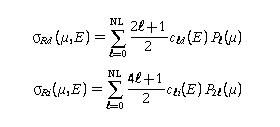
A cross section value of 1.0 is used in File 3. Because the interference term oscillates as μ goes to 1, the limit of the Legendre representation of the residual cross section at small angles may not be well defined. However, if the coefficients are chosen properly, the effect of this region will be small due to the large magnitude of the Coulomb term.

It is also possible to represent experimental data using the nuclear plus interference representation. The cross section for File 3 and the angular distribution for File 6 are defined as follows:

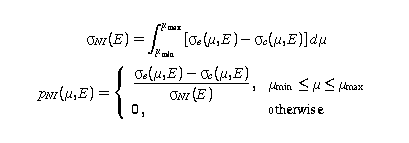
where μ_min is -1 for distinguishable particles and 0 for identical particles. The maximum cosine should be as close to 1.0 as possible, especially at high energies where Coulomb scattering is less important. The Coulomb cross section σ_C(μ,E) is to be computed using one of the first two equations on the page, depending on whether distinguishable or identical particles are being considered.

The following quantities are defined for LAW=5:

SPI

spin of the particle. Used for identical particles (SPI = 0, 1/2, 1, etc.).

LIDP

flag that indicates that the particles are identical when LIDP=1; otherwise, LIDP=0.

LTP

flag that indicates the representation:
LTP=1, nuclear amplitude expansion;
LTP=2, residual cross section expansion as Legendre coefficients;
LTP=12, nuclear plus interference distribution with lnp_NI linear in μ; and
LTP=14, nuclear plus interference distribution with p_NI linear in μ.

NR,NE,EINT

standard TAB2 parameters

NL

for LTP<3, NL is the highest Legendre order of nuclear partial waves used; and
for LTP>2, NL is the number of cosine tabulated.

NW

number of parameters given in the LIST record:
for LTP=1 and LIDP=0, use NW=4*NL+3;
for LTP=1 and LIDP=1, use NW=3*NL+3;
for LTP=2, use NW=NL+1; and
for LTP>2, use NW=2*NL.

AL(E)

coefficients a_i, b_i, or c_i in barns/sr as described below, or μ,p pairs with p dimensionless

     [MAT, 6, MT/ SPI, 0.0, LIDP, 0, NR, NE/ EINT] TAB2
     [MAT, 6, MT/ 0.0, E1, LTP, 0, NW, NL/ AL(E)] LIST
                  --------------------
                  continue with LIST records for the
                  rest of the NE incident energies
                  --------------------

LTP=1 and LIDP=0

b₀, b₁, ... b_2*NL, Ra₀, Ia₀, Ra₁, Ia₁, ...Ia_NL;

LTP=1 and LIDP=1

b₀, b₁, ... b_NL, Ra₀, Ia₀, Ra₁, Ia₁, ...Ia_NL;

LTP=2

c₀, c₁, ... c_NL; and

LTP>2

μ₁, p_NI(μ₁), ... μ_NL, p_NI(μ_NL),