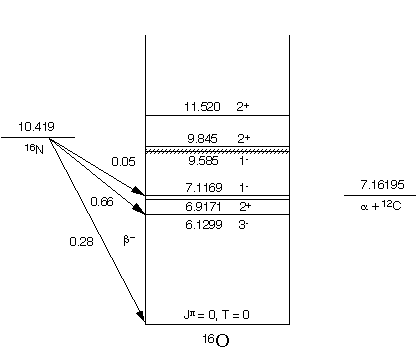
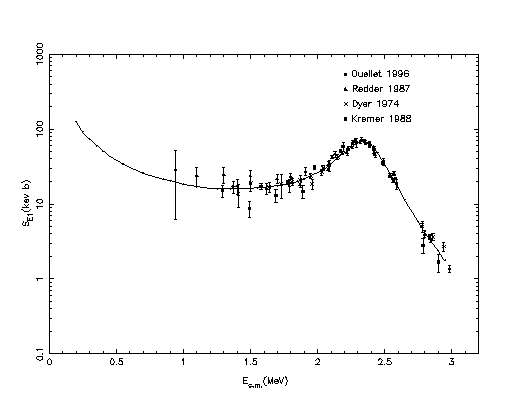
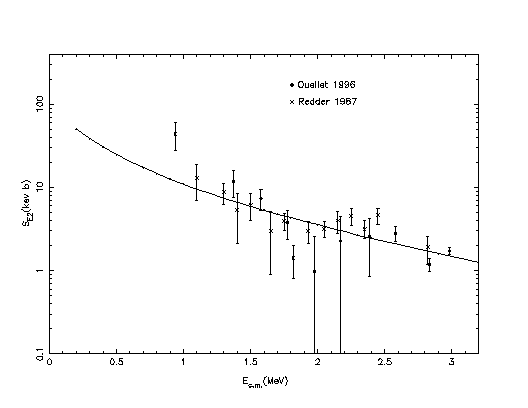
|
- [Ajz90]
- Ajzenberg-Selove, F., 1990, Nucl. Phys. A506, 1.
- [Bar71]
- Barker, F. C., 1971, Austr. J. Phys. 24, 777.
- [Bar87]
- Barker, F. C., 1987, Austr. J. Phys. 40, 25.
- [Bar91]
- Barker, F. C., and T. Kajino, 1991, Aust. J. Phys. 44, 369.
- [Buc93]
- Buchmann, L., R. E. Azuma, C. A. Barnes, J. M. D'Auria,
M. Dombsky, U. Giesen, K. P. Jackson, J. D. King, R. G. Korteling,
P. McNeely, J. Powell, G. Roy, J. Vincent, T. R. Wang, S. S. M. Wong
and P. R. Wrean, 1993, Phys. Rev. Lett. 70, 7026;
Azuma R. E., L. Buchmann, F. C. Barker, C. A. Barnes, J. M. D'Auria,
M. Dombsky, U. Giesen, K. P. Jackson, J. D. King, R. G. Korteling,
P. McNeely, J. Powell, G. Roy, J. Vincent, T. R. Wang, S. S. M. Wong
and P. R. Wrean, 1994, Phys. Rev. C 50, 1194.
- [Buc96]
- Buchmann, L., R. E. Azuma, C. A. Barnes, J. Humblet and K. Langanke,
1996, Phys. Rev. C 54, 393.
- [Dye74]
- Dyer, P. and C. A. Barnes, 1974, Nucl. Phys. A233, 495.
- [Fil89]
- Filippone, B. W., J. Humblet, and K. Langanke, 1989, Phys. Rev. C
40, 515.
- [Fow75]
- Fowler, W. A., G. R. Caughlin, and B. A. Zimmerman, 1975,
Ann. Rev. Astr. Ap. 13, 69.
- [Fra96]
- France, R. H. III, E. L. Wilds, N. B. Jevtic, J. E. McDonald,
and M. Gai, Proceedings, Nuclei in the Cosmos 1996, Nucl. Phys. A
(inpress), and private communication.
- [Hal96]
- Hale, G. M., 1966, Proceedings, Nuclei in the Cosmos 1996,
Nucl. Phys. A (inpress).
- ]Hoy53]
- Hoyle, F., D. N. F. Dunbar, W. A. Wenzel, and W. Whaling, 1953,
Phys. Rev. 92, 1095.
- [Hum91]
- Humblet, J., B. W. Filippone, and S. E. Koonin, 1991,
Phys. Rev. C 44, 2530.
- [Kie96]
- Kiener, J., V. Tatischeff, P. Aguer, G. Bogaert, A. Coc, D. Disdier,
L. Kraus, A. Lefebvre, I. Linck,W. Mittif, T. Motobayashi,
F. de Oliveira-Santos, P. Roussel-Chomaz, C. Stephan and J. P. Thibaud,
1996, Proceedings, Nuclei in the Cosmos 1996, Nucl. Phys. (inpress).
- [Koo74]
- Koonin, S. E., T. A. Tombrello and G. Fox, 1974,
Nucl. Phys. A220, 221.
- [Kre88]
- Kremer, R. M., C. A. Barnes, K. H. Chang, H. C. Evans, B. W. Fillipone,
K. H. Hahn and L. W. Mitchell, 1988, Phys. Rev. Lett. 60, 1475.
- [Oue92]
- Ouellet, J. M. L., H. C. Evans, H. W. Lee, J. R. Leslie, J. D. McArthur,
W. McLatchie, H.-B. Mak, P. Skensved, X. Zhao and T. K. Alexander, 1992,
Phys. Rev. Lett. 69, 1896.
- [Oue96]
- Ouellet, J. M. L., M. N. Butler, H. C. Evans, H. W. Lee, J. R. Leslie,
J. D. McArthur, W. McLatchie, H.-B. Mak, P. Skensved, J. L. Whitton,
and X. Zhao, 1996, Phys. Rev. C 54, 1982.
- [Neu74]
- Neubeck, K., H. Schober, and H. Wäffler, 1974, Phys. Rev. C 10,
320; Hättig, H., K. Hünchen, and H. Wä:ffler, 1970, Phys. Rev. Lett.
25, 941.
- [Pla87]
- Plaga, R., H. W. Becker, A. Redder, C. Rolfs, H. P. Trautvetter and
K. Langanke, 1987, Nucl. Phys. A465, 291; Plaga, R., 1986,
Diploma thesis (University of Münster).
- [Red87]
- Redder, A., H. W. Becker, C. Rolfs, H. P. Trautvetter, T. R. Donoghue,
T. C. Rinkel, J. W. Hammer and K. Langanke, 1987, Nucl. Phys. A462,
385.
- [Rol88]
- Rolfs, C. and W. S. Rodney, 1988, Cauldrons in the Cosmos
(University of Chicago Press, Chicago).
- [Til93]
- Tilley, D. R., H. R. Weller, and C. M. Cheves, 1993, Nucl. Phys.
A564,1.
- [Tra96]
- Trautvetter, H. P., G. Roters, C. Rolfs, S. Schmidt and P. Descouvemont,
1996, Proceedings, Nuclei in the Cosmos 1996, Nucl. Phys. (inpress).
- [Wea93]
- Weaver, T. A., and S. E. Woosley, 1993, Phys. Reports 227, 65.
- [Zha93]
- Zhao, Z., R. H. France III, K. S. Lai, S. L. Rugari, M. Gai and
E. L. Wilds, 1993, Phys. Rev. Lett. 70, 2066; Zhao, Z., 1993,
Ph. D. thesis (Yale University).
- [Zha95]
- Zhao, Z., E. Adelberger, and L. Debrackeler, 1995, U. Washington,
unpublished.
|
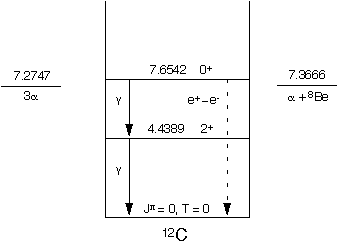
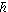 2/
(MαkT))3
(Γ
α
Γrad/
(
2/
(MαkT))3
(Γ
α
Γrad/
(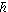 Γ))
exp(-Q/(kT)),
Γ))
exp(-Q/(kT)),
 Γ
α
≅ Γ,
the triple-alpha rate depends only on
Γrad=
Γ
γ+
&/Gamma;pair. The current
values [Ajz90] of these widths are
Γ
γ=
(3.64 +/- 0.50) meV and
Γpair=(60.5 +/- 3.9)
μeV. The
under-estimation of this rate by B2FH due to their value of
Γ
γ=1 meV was
compensated in part by having at that time a smaller Q-value (372 keV)
in the exponential factor in the rate equation.
Γ
α
≅ Γ,
the triple-alpha rate depends only on
Γrad=
Γ
γ+
&/Gamma;pair. The current
values [Ajz90] of these widths are
Γ
γ=
(3.64 +/- 0.50) meV and
Γpair=(60.5 +/- 3.9)
μeV. The
under-estimation of this rate by B2FH due to their value of
Γ
γ=1 meV was
compensated in part by having at that time a smaller Q-value (372 keV)
in the exponential factor in the rate equation.